相机标定的原理
非线性畸变的来源

摄像机光学系统的透镜组不完善造成的径向畸变
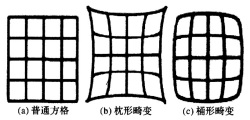
透镜系统的远光轴区域的放大率与光轴附近的放大率差异导致图像上的点向内或向外偏离光轴中心,若远光轴区域的放大率比光轴附近的大,则造成枕形畸变,若小于光轴附近的放大率,则造成桶形畸变。
前两阶畸变量可以表示为:
$$\begin{cases} δ_u=k_1u(u^2+v^2)+k_2u(u^2+v^2)^2 \\ δ_v=k_1v(u^2+v^2)+k_2v(u^2+v^2)^2 \end{cases}$$
不正确的镜头组合引起离心畸变
实际相机的光学系统的光学中心和镜头各器件的光学中心不一致带来的畸变,既包含径向畸变也包含切向畸变。
前两阶畸变量可表示为:
$$\begin{cases} δ_u=p_1(3u^2+v^2)+2p_2uv \\ δ_v=p_2(u^2+3v^2)+2p_1uv \end{cases}$$
摄像机装配不完善造成薄透镜畸变(影响较小)
透镜设计、生产不完善和安装误差造成的畸变,包含径向畸变和切向畸变。
通常取一阶畸变量即可:
$$\begin{cases} δ_u=q_1(u^2+v^2)\\ δ_v=q_2(u^2+v^2) \end{cases}$$
建立畸变模型
一般情况下建立畸变模型只需考虑主要畸变,取1个或两个主要畸变来源即可,高阶畸变量相对来说影响很小,可以忽略,因此此处建立的畸变模型仅包含一、二阶径向畸变和一、二阶离心畸变:
$$\begin{cases} x_d=x_u+ x_u(k_1r_u^2+k_2r_u^4)+p_1(r_u^2+2 x_u^2)+2p_2 x_u y_u \\ y_d=y_u+ y_u(k_1r_u^2+k_2r_u^4)+p_2(r_u^2+2 y_u^2)+2p_1 x_u y_u \end{cases}$$
其中$r_u^2=x_u^2+y_u^2$。
求解畸变参数
根据标定板数据可知世界坐标系下各个角点(靶标)的理论位置,利用无畸变模型求出的内外参,计算出各角点重投影误差,进行非线性优化(牛顿高斯法,Levenberg算法,LM等)找到畸变参数$k_1、k_2、p_1、p_2$的最优解:
$$min||m_i-\hat{m_i}(dx,dy,u_0,v_0,k_1,k_2,p_1,p_2)||$$